[디지털비즈온 박종호 기자] 전에 이야기했었던 중심극한정리를 간단히 시각화해보겠습니다. 프로그램 툴로는 STATA를 이용해보겠습니다.

일반적인 동전이 있다고 해 봅시다. 한 번 던졌을 때 앞면이 나올 확률은 50%이고, 앞면(성공) 혹은 뒷면(실패)의 두 경우 외에 다른 경우의 수가 존재하지 않습니다. 따라서 동전을 던졌을 때 각 시행의 분포는 이항 분포를 따릅니다.

이항 분포는 여러 번의 독립적 시행 (동전을 한 번 던졌을 때의 결과가 다음 시행의 결과에 영향을 미치지 않습니다)에서 각 시행이 확률 p를 가질 때의 이산확률분포입니다. 여기서의 확률 p는 50%겠네요. 

따라서 동전을 한 번 던진다고 했을 때의 코드는 다음과 같습니다. binomial이 이항분포를 나타내는 코드이며, 편의상 앞면을 1, 뒷면을 0이라고 하겠습니다.

clear

set seed 12345

set obs 1

gen x = rbinomial(1, .5)

tab x

동전을 10번 던진다고 해 봅시다. 랜덤으로 같은 동작을 10번 반복하라는 매크로 코드를 입력해 보겠습니다.

clear

set seed 12345

set obs 10

gen x = .

forvalues n = 1(1)10 {

replace x = rbinomial(1, .5)

}

list x
 

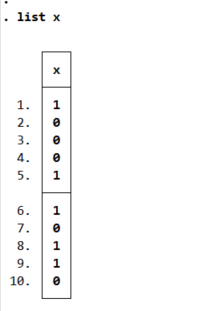
그 결과 앞면(1)이 다섯 번 나왔네요. 예상대로입니다. 같은 방식으로 동전을 100번, 1000번, 10000번도 던지라고 지시할 수 있습니다.

그렇다면 중심극한정리를 시험해보겠습니다. 표본의 수가 많아질수록 표본평균의 분포는 정규분포에 가까워진다는 정리입니다. 동전을 1번, 2번, 3번.... 10번까지 던져보겠습니다. 그리고 각 시행에서 나온 앞면의 횟수와 확률을 하나의 표본으로 하겠습니다. 총 표본의 갯수는 10개가 되겠네요.

set seed 12345

clear

set obs 10000

gen pihat=.

local i = 1

forvalues n = 1(1)10000 {

gen x = rbinomial(`n', .5)

su x 

replace pihat = r(mean)/`n' in `i+'

drop x

local i=`i'+1

}

kdensity pihat

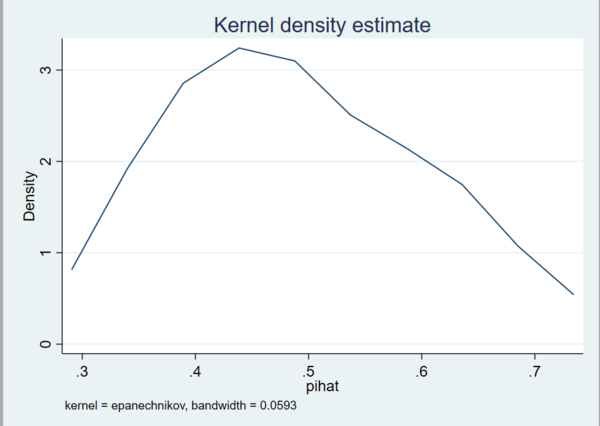
표본의 갯수가 너무 적은 탓인지, 정규분포와는 조금 거리가 먼 모양입니다. 무엇보다도 그래프의 고점이 평균인 0.5보다 작은 모양새입니다. 고점을 중심으로 그래프의 좌우도 모양이 다릅니다.

이번에는 표본의 갯수를 20개로 늘려보겠습니다.

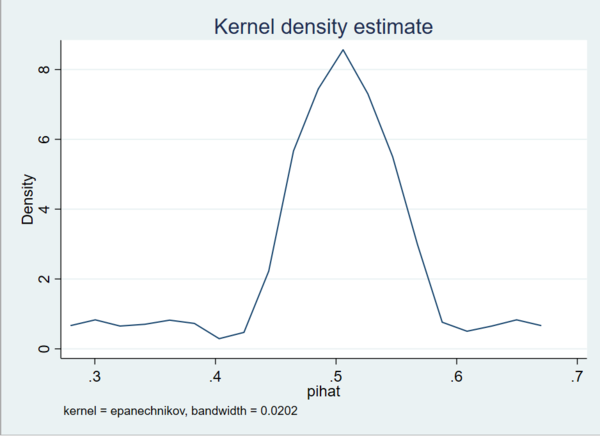
정규분포와 얼추 비슷한 모양이 나온 것 같지만, 그래도 좀 울퉁불퉁합니다. 이번엔 30개로 늘려보겠습니다.
 

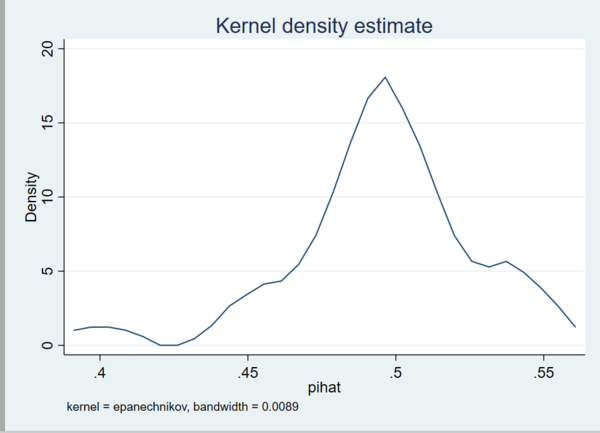
조금 더 종모양에 가까워진 것 같습니다. 이번에는 100개로 늘려보겠습니다.

 

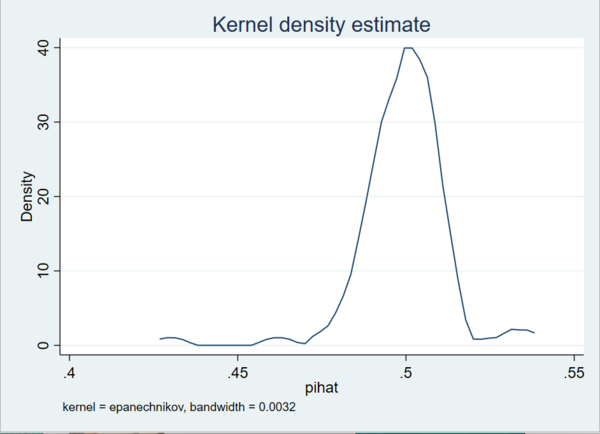
각 점들의 분포가 평균을 중심으로 모이는 모양새입니다. 정규분포에 가까워지는 것은 물론, 표본평균이 모평균에 수렴한다는 사실까지 눈으로 확인할 수 있습니다. 마지막으로 표본의 갯수를 1000개로 늘려보겠습니다.
 

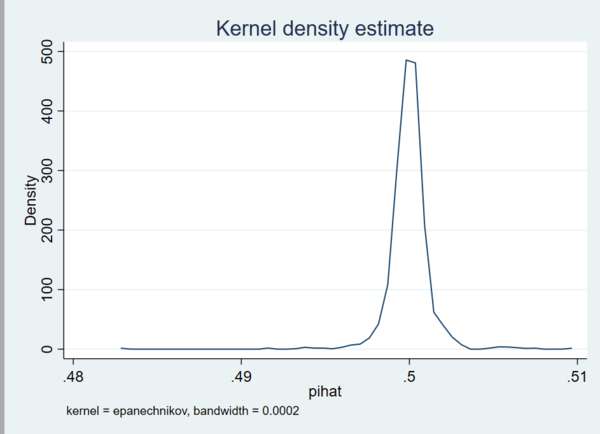
정규분포와 매우 흡사한 그래프가 나왔습니다. 평균인 0.5를 중심으로 대단히 많은 데이터(각 표본)가 모여있음을 확인할 수 있습니다 (가운데가 아주 뾰족한 모양입니다) 아울러 표본의 갯수가 100개일 때와 비교해 분산 역시 매우 작아졌습니다. 앞선 그래프가 평균 0.45에서 0.55를 중심으로 분포되었다면, 이번에는 0.49에서 0.51 사이에서 대부분의 데이터가 모여있습니다.

표본의 갯수가 많으면 많을수록 데이터의 신뢰도가 높아짐을 알 수 있습니다. 우리가 데이터 분석을 할 때, 대체로 많은 샘플의 갯수에 집착하는 이유도 이와 같습니다. 우리가 흔히 말하는 빅데이터를 신뢰하는 이유도 결국 샘플의 갯수가 많기(big) 때문입니다.